login/create account
Let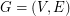 
be a graph. If 
and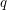 
are two integers, a 
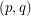-colouring of 
is a function 
from 
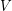to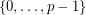 
such that 
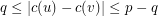for each edge 
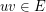. Given a list assignment 
of , i.e.~a mapping that assigns to every vertex 
a set of non-negative integers, an -colouring of is a mapping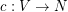 
such that 
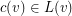for every 
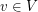. A list assignment is a 
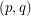--list-assignment if 
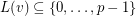and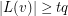 
for each vertex 
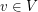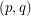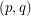. Given such a list assignment , the graph G is --colourable if there exists a --colouring , i.e. is both a 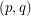-colouring and an -colouring. For any real number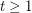 
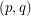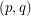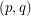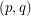, the graph is --choosable if it is --colourable for every --list-assignment . Last, is circularly -choosable if it is --choosable for any , 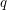. The circular choosability (or circular list chromatic number or circular choice number) of G is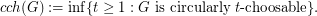 
Problem What is the best upper bound on circular choosability for planar graphs?
The problem was first posed in 2003 by Mohar (Problem 4 of link*) who suggested the answer should be between 4 and 5.
Some time later, Havet, Kang, Müller, and Sereni [HKMS] showed that in fact the answer is somewhere between 6 and 8. The upper bound extends a celebrated planar choosability proof due to Thomassen [T]. The lower bound is by way of an elementary, though rather large, construction.
Bibliography
[HKMS] F. Havet, R. J. Kang, T. Müller, and J.-S. Sereni. Circular choosability. J. Graph Theory 61 (2009), no. 4, 241--270.
[T] C. Thomassen. Every planar graph is 5-choosable. J. Combinatorial Theory B 62 (1994) 180--181
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University