Case 2: If all of the edges of the form are contained in the same cycle in a 2-factor of , then replacing the edges with the edges converts this 2-factor of into a 2-factor of disjoint copies of the Petersen graph. Hence, when restricted to each , the 2-factor of consists of a cycle with 5 vertices and a -path containing a total of 5 vertices. These paths must be joined together through the edges of the form creating a cycle of length 5n. Hence, in this case the 2-factor of contains cycles of length 5 and one cycle of length 5n (which is odd).
Now, is a bridgeless cubic graph whose 2-factors contain only odd cycles, but no 2-factor of contains fewer than cycles.
This conecture is false.
Case 2: If all of the edges of the form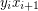 are contained in the same cycle in a 2-factor of
are contained in the same cycle in a 2-factor of 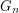 , then replacing the edges
, then replacing the edges 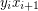 with the edges
with the edges 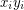 converts this 2-factor of
converts this 2-factor of 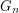 into a 2-factor of
into a 2-factor of  disjoint copies of the Petersen graph. Hence, when restricted to each
disjoint copies of the Petersen graph. Hence, when restricted to each 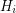 , the 2-factor of
, the 2-factor of 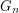 consists of a cycle with 5 vertices and a
consists of a cycle with 5 vertices and a 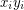 -path containing a total of 5 vertices. These paths must be joined together through the edges of the form
-path containing a total of 5 vertices. These paths must be joined together through the edges of the form 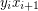 creating a cycle of length 5n. Hence, in this case the 2-factor of
creating a cycle of length 5n. Hence, in this case the 2-factor of 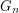 contains
contains  cycles of length 5 and one cycle of length 5n (which is odd).
cycles of length 5 and one cycle of length 5n (which is odd).
Now,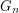 is a bridgeless cubic graph whose 2-factors contain only odd cycles, but no 2-factor of
is a bridgeless cubic graph whose 2-factors contain only odd cycles, but no 2-factor of 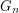 contains fewer than
contains fewer than 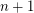 cycles.
cycles.