For odd and , let be the graph obtained by deleting an edge, say , from the Petersen graph. Define to be the graph obtained by joining vertex and vertex with an edge (with subscripts reduced modulo ). For each , the set is an edge cut. Hence, in any 2-factor of , either none of the edges of the form are contained in a cycle, or all of them are contained in the same cycle.
Case 1: If none of the edges described above are contained in a cycle of a 2-factor of , then this 2-factor contains a 2-factor of for each . These 2-factors are also 2-factors of the graphs , that is, each is a 2-factor of the Petersen graph. Each 2-factor of the Petersen graph consists of two cycles of 5 vertices, hence, any such 2-factor of contains cycles of odd length.
This conjecture is false.
For odd and
and ![$ i\in[n] $](/files/tex/3489ac3673ff1a2165798412b5aaf3c992a55253.png) , let
, let 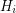 be the graph obtained by deleting an edge, say
be the graph obtained by deleting an edge, say 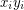 , from the Petersen graph. Define
, from the Petersen graph. Define 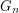 to be the graph obtained by joining vertex
to be the graph obtained by joining vertex 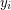 and vertex
and vertex 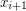 with an edge (with subscripts reduced modulo
with an edge (with subscripts reduced modulo  ). For each
). For each ![$ i\in[n] $](/files/tex/3489ac3673ff1a2165798412b5aaf3c992a55253.png) , the set
, the set 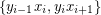 is an edge cut. Hence, in any 2-factor of
is an edge cut. Hence, in any 2-factor of 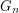 , either none of the edges of the form
, either none of the edges of the form 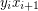 are contained in a cycle, or all of them are contained in the same cycle.
are contained in a cycle, or all of them are contained in the same cycle.
Case 1: If none of the edges described above are contained in a cycle of a 2-factor of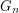 , then this 2-factor contains a 2-factor of
, then this 2-factor contains a 2-factor of 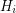 for each
for each 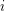 . These 2-factors are also 2-factors of the graphs
. These 2-factors are also 2-factors of the graphs 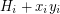 , that is, each is a 2-factor of the Petersen graph. Each 2-factor of the Petersen graph consists of two cycles of 5 vertices, hence, any such 2-factor of
, that is, each is a 2-factor of the Petersen graph. Each 2-factor of the Petersen graph consists of two cycles of 5 vertices, hence, any such 2-factor of 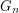 contains
contains 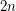 cycles of odd length.
cycles of odd length.
Case 2: See the comment below.