Home » Subject » Graph Theory » Coloring » Vertex coloring
Importance: Medium ✭✭
Author(s): Erdos, Paul
Lovasz, Laszlo
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: coloring
complete graph
Recomm. for undergrads: no
Posted by: DFR
on: January 18th, 2009

A connected simple graph $ G $ is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.

Conjecture   $ K_n $ is the only $ n $-chromatic double-critical graph

This conjecture is a special case of a more general problem by Erdos and Lovasz proposed in 1966. It has been independently proven for the case where 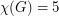$ \chi(G) = 5 $ by Mozhan [3] and Stiebitz [4].

Bibliography

*[1] P. Erdos, Problem 2, in: Theory of Graphs (Proc. Colloq., Tihany, 1966), Academic Press, New York, 1968, p. 361.

[2] F. Chung, R. Graham, Erdos on graphs: His legacy of unsolved problems, A K Peters, Wellesley, Massachusetts, 1998.

[3] N. N. Mozhan, On double critical graphs with the chromatic number five, Metody Diskretb. Anal. 46 (1987) 50-59.

[4] M. Stiebitz, 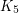$ K_5 $ is the only double-critical $ 5 $-chromatic graph, Discrete Math. 64 (1987) 91-93.


* indicates original appearance(s) of problem.
2 comments

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options