 login/create account
login/create account
Conjecture Let  be a simple
be a simple  -uniform hypergraph, and assume that every set of
-uniform hypergraph, and assume that every set of 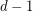 points is contained in at most
points is contained in at most  edges. Then there exists an
edges. Then there exists an 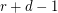 -edge-coloring so that any two edges which share
-edge-coloring so that any two edges which share 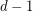 vertices have distinct colors.
vertices have distinct colors.
 be a simple
be a simple  -uniform hypergraph, and assume that every set of
-uniform hypergraph, and assume that every set of 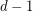 points is contained in at most
points is contained in at most  edges. Then there exists an
edges. Then there exists an 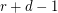 -edge-coloring so that any two edges which share
-edge-coloring so that any two edges which share 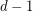 vertices have distinct colors.
vertices have distinct colors. Vizing's Theorem is equivalent to the above statement for 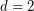 . For higher dimensions, this problem looks difficult since the main tool used in the proof of Vizing's theorem (Kempe chains) do not appear to work.
. For higher dimensions, this problem looks difficult since the main tool used in the proof of Vizing's theorem (Kempe chains) do not appear to work.

 Drupal
Drupal CSI of Charles University
CSI of Charles University