 login/create account
login/create account
Let  be a positive integer. We say that a graph
be a positive integer. We say that a graph  is strongly
is strongly  -colorable if for every partition of the vertices to sets of size at most
-colorable if for every partition of the vertices to sets of size at most  there is a proper
there is a proper  -coloring of
-coloring of  in which the vertices in each set of the partition have distinct colors.
in which the vertices in each set of the partition have distinct colors.
Conjecture If 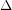 is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 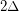 -colorable.
-colorable.
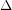 is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 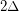 -colorable.
-colorable. Haxell proved that if 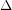 is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 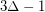 -colorable. She later proved that the strong chromatic number
-colorable. She later proved that the strong chromatic number 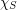 is at most
is at most 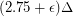 for sufficiently large
for sufficiently large 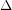 depending on
depending on  . Aharoni, Berger, and Ziv proved the fractional relaxation.
. Aharoni, Berger, and Ziv proved the fractional relaxation.

 Drupal
Drupal CSI of Charles University
CSI of Charles University