 login/create account
login/create account
Conjecture If  is an invertible
is an invertible 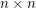 matrix, then there is an
matrix, then there is an 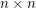 submatrix
submatrix 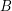 of
of ![$ [A A] $](/files/tex/d1e9d82c656535b507686183e640178057fae455.png) so that
so that 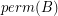 is nonzero.
is nonzero.
 is an invertible
is an invertible 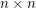 matrix, then there is an
matrix, then there is an 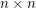 submatrix
submatrix  of
of ![$ [A A] $](/files/tex/d1e9d82c656535b507686183e640178057fae455.png) so that
so that 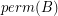 is nonzero.
is nonzero. If true, this conjecture would imply the nowhere-zero point in a linear mapping conjecture via the Alon-Tarsi polynomial technique. I believe Yang Yu was the first to suggest the following generalization of the permanent conjecture.
Conjecture (Yu) If 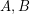 are invertible
are invertible 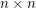 matrices over the same field, then there is an
matrices over the same field, then there is an 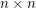 submatrix
submatrix  of
of ![$ [A B] $](/files/tex/36e5a5f00d293482873baeba6adb9f63be8b272e.png) so that
so that 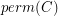 is nonzero.
is nonzero.
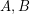 are invertible
are invertible 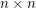 matrices over the same field, then there is an
matrices over the same field, then there is an 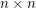 submatrix
submatrix  of
of ![$ [A B] $](/files/tex/36e5a5f00d293482873baeba6adb9f63be8b272e.png) so that
so that 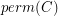 is nonzero.
is nonzero. This conjecture when restricted to the field 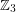 is a consequence of the Alon-Tarsi basis conjecture. In addition to implying the above conjecture, the truth of this conjecture for matrices over the field
is a consequence of the Alon-Tarsi basis conjecture. In addition to implying the above conjecture, the truth of this conjecture for matrices over the field 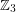 would imply that every 6-edge-connected graph has a nowhere-zero 3-flow, thus resolving The weak 3-flow conjecture.
would imply that every 6-edge-connected graph has a nowhere-zero 3-flow, thus resolving The weak 3-flow conjecture.

 Drupal
Drupal CSI of Charles University
CSI of Charles University