 login/create account
login/create account
Conjecture For every prime  , there is a constant
, there is a constant 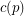 (possibly
(possibly 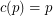 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 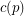 bases of the vector space
bases of the vector space 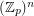 contains an additive basis.
contains an additive basis.
 , there is a constant
, there is a constant 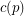 (possibly
(possibly 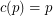 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 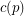 bases of the vector space
bases of the vector space 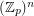 contains an additive basis.
contains an additive basis. Definition: Let 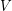 be a finite dimensional vector space over the field
be a finite dimensional vector space over the field 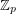 . We call a multiset
. We call a multiset 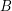 with elements in
with elements in 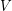 an additive basis if for every
an additive basis if for every 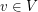 , there is a subset of
, there is a subset of 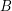 which sums to
which sums to  .
.
It is worth noting that this conjecture would also imply that every 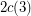 -edge-connected graph has a nowhere-zero 3-flow, thus resolving The weak 3-flow conjecture.
-edge-connected graph has a nowhere-zero 3-flow, thus resolving The weak 3-flow conjecture.

 Drupal
Drupal CSI of Charles University
CSI of Charles University