 login/create account
login/create account
Sheehan, John
r-regular graphs are not uniquely hamiltonian. ★★★
Author(s): Sheehan
Conjecture If  is a finite
is a finite  -regular graph, where
-regular graph, where 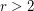 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian.
 is a finite
is a finite  -regular graph, where
-regular graph, where 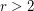 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian. Keywords: hamiltonian; regular; uniquely hamiltonian

 Drupal
Drupal CSI of Charles University
CSI of Charles University