 login/create account
login/create account
Meshulam, Roy
The Alon-Tarsi basis conjecture ★★
Author(s): Alon; Linial; Meshulam
Conjecture If 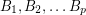 are invertible
are invertible 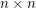 matrices with entries in
matrices with entries in 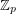 for a prime
for a prime  , then there is a
, then there is a 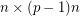 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base.
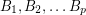 are invertible
are invertible 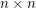 matrices with entries in
matrices with entries in 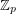 for a prime
for a prime  , then there is a
, then there is a 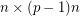 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base. Keywords: additive basis; matrix

 Drupal
Drupal CSI of Charles University
CSI of Charles University