 login/create account
login/create account
Gonshor, Harry
Length of surreal product ★
Author(s): Gonshor
Conjecture Every surreal number has a unique sign expansion, i.e. function 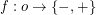 , where
, where  is some ordinal. This
is some ordinal. This  is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of
is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of  as
as 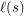 .
.
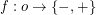 , where
, where  is some ordinal. This
is some ordinal. This  is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of
is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of  as
as 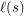 .
.
It is easy to prove that
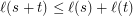
What about
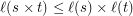
?
Keywords: surreal numbers

 Drupal
Drupal CSI of Charles University
CSI of Charles University