 login/create account
login/create account
spanning trees (Solved)
Problem Prove or disprove: Let  be a graph with the minimum vertex degree at least 2; that is,
be a graph with the minimum vertex degree at least 2; that is, 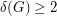 . Then there exists a spanning tree
. Then there exists a spanning tree  of
of  such that for every support vertex
such that for every support vertex  in
in  if
if 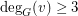 , then
, then 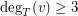 .
.
 be a graph with the minimum vertex degree at least 2; that is,
be a graph with the minimum vertex degree at least 2; that is, 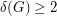 . Then there exists a spanning tree
. Then there exists a spanning tree  of
of  such that for every support vertex
such that for every support vertex  in
in  if
if 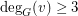 , then
, then 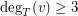 .
. A computer search shows that the claim is true for every graph of order at most 8 and minimum vertex degree at least 2.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Solution by Ruben van der Zwaan
Where is the solution posted?