 login/create account
login/create account
Random stable roommates
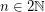 people admits a solution is
people admits a solution is 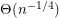 .
. A system of preferences for a graph  is a family
is a family 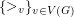 so that every
so that every 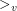 is a linear ordering of the neighbors of the vertex
is a linear ordering of the neighbors of the vertex  . We say that
. We say that  prefers
prefers  to
to 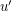 if
if 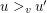 . A perfect matching
. A perfect matching  in
in  is stable if there do not exist
is stable if there do not exist 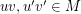 so that
so that  prefers
prefers 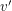 to
to  and
and 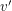 prefers
prefers  to
to 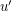 .
.
A famous theorem of Gale-Shapley [GS] proves that every system of preferences on a complete bipartite graph 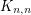 admits a stable perfect matching. Indeed, they provide an amusing algorithm to construct one. On complete graphs, this problem is known as either the homosexual stable marriage problem, or more commonly, the stable roommate problem. Here there does not always exist a solution (that is, a stable perfect matching), but Irving [I] constructed an algorithm which runs in polynomial time, and outputs a solution if one exists.
admits a stable perfect matching. Indeed, they provide an amusing algorithm to construct one. On complete graphs, this problem is known as either the homosexual stable marriage problem, or more commonly, the stable roommate problem. Here there does not always exist a solution (that is, a stable perfect matching), but Irving [I] constructed an algorithm which runs in polynomial time, and outputs a solution if one exists.
Let 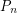 denote the probability that a random instance of the stable roommates problem has a solution (so the above conjecture asserts that
denote the probability that a random instance of the stable roommates problem has a solution (so the above conjecture asserts that 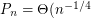 ). The following are the best known asymptotic bounds for
). The following are the best known asymptotic bounds for 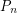 (with
(with  even) and hold for
even) and hold for  sufficiently large. The lower bound is due to Pittel [P] and the upper bound to Pittel and Irving [IP]
sufficiently large. The lower bound is due to Pittel [P] and the upper bound to Pittel and Irving [IP]
![\[ \frac{2 e ^{3/2} }{ \sqrt{\pi n}} \le P_n \le \frac{\sqrt{e}}{2} \]](/files/tex/b60e73cca91e713acba7d032e33d21b611e9e002.png)
Mertens [M] did an extensive Monte-Carlo simulation to obtain the above conjecture. Indeed, by guessing at the constant he even offers the stronger conjecture 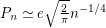 .
.
Bibliography
[GS] D. Gale D and L. S. Shapley, College admissions and the stability of marriage, Am. Math. Mon. 69 9-15.
[I] R. W. Irving, An efficient algorithm for the stable roommates problem, J. Algorithms 6 577-95.
[IP] B. Pittel and R. W. Irving, An upper bound for the solvability of a random stable roommates instance, Random Struct. Algorithms 5 465-87.
*[M] S. Mertens, Random stable matchings, J. Stat. Mech. Theory Exp. 2005, no. 10 MathSciNet
[P] B. Pittel, The 'stable roommates' problem with random preferences, Ann. Probab. 21 1441-77
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University