 login/create account
login/create account
Perfect cuboid
Perfect cuboid is a cuboid whose edges and face and body diagonals are all integers. In other words, is there any solution to the following system of Diophantine equations:
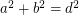
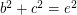
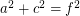
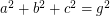
Bibliography
* indicates original appearance(s) of problem.
well, I'll bite...
If you still think you have a proof, I'd love to take a look - my email is timro21@gmail.com, or you could have it published on the Unsolved Problems web site at http://www.unsolvedproblems.org/
Tim
Is there any 4D Euler brick?
Perfect cuboid is related to Euler brick whose edges and face diagonals are all integers. It is know that there are infinite Euler bricks. But is there any 4D Euler brick? In other words, is there any solution to the following system of Diophantine equations:
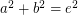
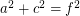
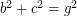
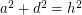
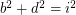
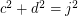
I computed a, b, c, d up to 1 million with brute force and found no solution. Any idea?
Divisibility
I found the divisibility conditions of four sides a, b, c and d in a primitive 4d euler brick (if exists):
1. One is divided by 64, another by 16, another by 4, another odd.
2. One is divided by 27, another by 9, another by 3, another not by 3.
3. Two is divided by 5.
4. Two is divided by 11.
5. One is divided by 13.
6. One is divided by 19.
Without loss of generality,
Without loss of generality, we can suppose a > b > c > d and remove a Diophantine equation from the system. I found some solutions, for example: without the last equation, the following quadruple is a solution. a=6325,b=5796,c=5520,d=528. They are so small, so i guess 4D euler bricks should exist.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Primitive perfect cuboid (Primitive perfect Euler brick)
I think that I have a simple proof that there cannot be any primitive perfect cuboid (primitive perfect Euler brick). I am willing to provide it if anyone requests it. T Herndon