Home » Subject » Graph Theory

Matching cut and girth

Importance: Medium ✭✭
Author(s):
Subject: Graph Theory
Keywords: matching cut, matching, cut
Recomm. for undergrads: no
Posted by: w
on: November 30th, 2011
Question   For every $ d $ does there exists a $ g $ such that every graph with average degree smaller than $ d $ and girth at least $ g $ has a matching-cut?

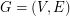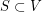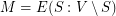Let $ G=(V,E) $ be a graph. A matching $ M $ is a matching-cut if there exists a set $ S\subset V $ such that $ M = E(S:V\setminus S) $. Graphs having a matching-cut are called decomposable.

It is known that every graph with 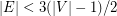$ |E| < 3(|V|-1)/2 $ is decomposable [BFP11].

Bibliography

[C84] V. Chvátal, Recognizing decomposable graphs, J Graph Theory 8 (1984), 51–53

[BFP11] P. Bonsma, A. Farley, A. Proskurowski, Extremal graphs having no matching cuts, J Graph Theory (2011)


* indicates original appearance(s) of problem.
add new comment