Home » Subject » Probability

KPZ Universality Conjecture

Importance: High ✭✭✭
Author(s):
Subject: Probability
Keywords: KPZ equation, central limit theorem
Recomm. for undergrads: no
Posted by: Tomas Kojar
on: October 3rd, 2020
Conjecture   Formulate a central limit theorem for the KPZ universality class.

The KPZ equation is given by

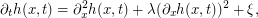
$$ \partial_{t}h(x,t)=\partial_{x}^{2}h(x,t)+\lambda(\partial_{x}h(x,t))^{2}+\xi, $$

where 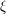$ \xi $ denotes space-time white noise and 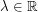$ \lambda\in \mathbb{R} $ is a parameter describing the strength of its "asymmetry". It has been conjectured (see [BPRS93, BG97, Cor 12 ,GJ14,HQ18] for a number of results in this direction) that the KPZ equation has a “universal” character in the sense that any one-dimensional model of surface growth should converge to it provided that it has the following features:

• There is a microscopic smoothing mechanism. Pictorially this means that large valleys are quickly filled.

• The system has microscopic fluctuations with short-range correlations. Pictorially this means that height function change depends only on neighboring heights.

• The system has some “lateral growth” mechanism in the sense that the growth speed depends in a nontrivial way on the slope. The vertical effective growth rate depends non-linearly on local slope.

• At the microscopic scale, the strengths of the growth and fluctuation mechanisms are well separated: either the growth mechanism dominates (intermediate disorder) or the fluctuations dominate (weak asymmetry). Growth is drive by noise which quickly decorrelates in space / time and is not heavy tailed.

Here is a concrete surface growth mathematical model to give a sense of the above features. The random deposition model is one of the simplest (and least realistic) models for a randomly growing one-dimensional interface. Unit blocks fall independently and in parallel from the sky above each site of $ \mathbb{Z} $ according to exponentially distributed waiting times. 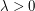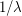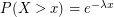Recall that a random variable X has exponential distribution of rate $ \lambda>0 $ (or mean $ 1/\lambda $) if $ P(X > x) = e^{-\lambda x} $. Such random variables are characterized by the memoryless property – conditioned on the event that 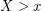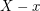$ X > x $, $ X - x $ still has the exponential distribution of the same rate. Consequently, the random deposition model is Markov – its future evolution only depends on the present state (and not on its history). The ballistic deposition (or sticky block) model was introduced by Vold [V59] in 1959 and, as one expects in real growing interfaces, displays spatial correlation. As before, blocks fall according to iid exponential waiting times, however, now a block will stick to the first edge against which it becomes incident. This creates overhangs and we define the height function h(t, x) as the maximal height above x which is occupied by a box.

Bibliography

[BG97] L. BERTINI and G. GIACOMIN. Stochastic Burgers and KPZ equations from particle systems. Comm. Math. Phys. 183, no. 3, (1997), 571–607.

[BPRS93] L. BERTINI, E. PRESUTTI, B. RUDIGER ¨ , and E. SAADA. Dynamical fluctuations at the critical point: convergence to a nonlinear stochastic PDE. Teor. Veroyatnost. i Primenen. 38, no. 4, (1993), 689–741

[Cor 12] I. Corwin, The Kardar-Parisi-Zhang equation and universality class, Random Matrices Theory Appl. 1 (2012), 1130001, 76. MR 2930377. Zbl 1247.82040. http://dx.doi.org

[GJ14] P. GONC¸ ALVES and M. JARA. Nonlinear fluctuations of weakly asymmetric interacting particle systems. Arch. Ration. Mech. Anal. 212, no. 2, (2014), 597–644

[HQ18] HAIRER, M. and QUASTEL, J. (2018). A class of growth models rescaling to KPZ. Forum Math. Pi 6 e3

[V59] M. J. Vold. A numerical approach to the problem of sediment volume. J. Colloid Sci., 14:168 (1959).


* indicates original appearance(s) of problem.
add new comment