 login/create account
login/create account
Infinite uniquely hamiltonian graphs
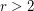 ?
? (Originally appeared as [M].)
Let  be a locally finite infinite graph and let
be a locally finite infinite graph and let 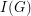 be the set of ends of~
be the set of ends of~ . The Freudenthal compactification of
. The Freudenthal compactification of  is the topological space
is the topological space 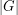 which is obtained from the usual topological space of the graph, when viewed as a 1-dimensional cell complex, by adding all points of
which is obtained from the usual topological space of the graph, when viewed as a 1-dimensional cell complex, by adding all points of 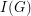 and setting, for each end
and setting, for each end 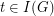 , the basic set of neighborhoods of
, the basic set of neighborhoods of  to consist of sets of the form
to consist of sets of the form 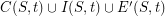 , where
, where  ranges over the finite subsets of
ranges over the finite subsets of 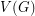 ,
, 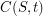 is the component of
is the component of 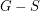 containing all rays in
containing all rays in  , the set
, the set 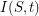 contains all ends in
contains all ends in 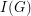 having rays in
having rays in 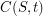 , and
, and 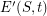 is the union of half-edges
is the union of half-edges ![$ (z,y] $](/files/tex/a5f38f582e42bda9e97013b03f0724fb550d8cf0.png) , one for every edge
, one for every edge 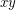 joining
joining  and
and 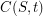 . We define a hamilton circle in
. We define a hamilton circle in 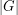 as a homeomorphic image
as a homeomorphic image  of the unit circle
of the unit circle 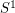 into
into 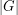 such that every vertex (and hence every end) of
such that every vertex (and hence every end) of  appears in
appears in  . More details about these notions can be found in [D].
. More details about these notions can be found in [D].
A graph  (finite or infinite) is said to be uniquely hamiltonian if it contains precisely one hamilton circle.
(finite or infinite) is said to be uniquely hamiltonian if it contains precisely one hamilton circle.
For finite graphs, the celebrated Sheehan's conjecture states that there are no  -regular uniquely hamiltonian graphs for
-regular uniquely hamiltonian graphs for 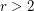 ; this is known for all odd
; this is known for all odd  and even
and even 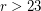 . For infinite graphs this is false even for odd
. For infinite graphs this is false even for odd  (e.g. for the two-way infinite ladder), but each of the known counterexamples has at least 2 ends, leading to the problem stated.
(e.g. for the two-way infinite ladder), but each of the known counterexamples has at least 2 ends, leading to the problem stated.
Another way to extend Sheehan's conjecture to infinite graphs is to define degree of an end 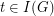 to be the maximal number of disjoint rays in
to be the maximal number of disjoint rays in  and ask the following:
and ask the following:
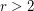 ?
? Bibliography
[D] R. Diestel, Graph Theory, Third Edition, Springer, 2005.
*[M] Bojan Mohar, Problem of the Month
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University