 login/create account
login/create account
Frankl's union-closed sets conjecture
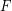 be a finite family of finite sets, not all empty, that is closed under taking unions. Then there exists
be a finite family of finite sets, not all empty, that is closed under taking unions. Then there exists  such that
such that  is an element of at least half the members of
is an element of at least half the members of 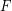 .
. This conjecture is notoriously difficult, even though (or should we say `because'?) it involves almost no mathematical structure whatsoever. It was posed by Frankl in the late 1970's. The recent paper of Morris [M] provides a good illustration of the kind of partial results known: Morris extends earlier work to show that the conjecture holds for families containing three 3-subsets of a 5-set, four 3-subsets of a 6-set, or eight 4-subsets of a 6-set. In a different direction, Czédli [C] has proved the conjecture in the case when 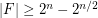 where
where 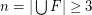 .
.
Bibliography
[C] G. Czédli, On averaging Frankl's conjecture for large union-closed-sets, J. Combin. Theory Ser. A, to appear.
[M] R. Morris, FC-families and improved bounds for Frankl's conjecture, European J. Combin. 27 (2006), no. 2, 269–282.
[P] B. Poonen, Union-closed families, J. Combin. Theory Ser. A 59 (1992), no. 2, 253–268.
[V] T. P. Vaughan, Three-sets in a union-closed family, J. Combin. Math. Combin. Comput. 49 (2004), 73–84.
[W] P. Wójcik, Union-closed families of sets, Discrete Math. 199 (1999), no. 1–3, 173–182.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Frankl's conjecture
For mor einformation and many references see also West's account in: http://www.math.uiuc.edu/~west/openp/unionclos.html