 login/create account
login/create account
Fowler's Conjecture on eigenvalues of (3,6)-polyhedra (Solved)
 be the graph of a
be the graph of a 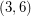 -polyhedron with
-polyhedron with 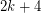 vertices. Then the eigenvalues of
vertices. Then the eigenvalues of  can be partitioned into three classes:
can be partitioned into three classes: 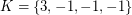 ,
, 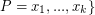 (where
(where 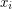 is nonnegative for
is nonnegative for 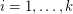 ), and
), and 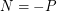 .
. A 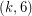 -polyhedron is a cubic graph embedded in the plane so that all of its faces are
-polyhedron is a cubic graph embedded in the plane so that all of its faces are  -gons or hexagons. Such graphs exist only for
-gons or hexagons. Such graphs exist only for 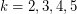 . The
. The 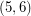 -polyhedra are also known as fullerene graphs since they correspond to the molecular graphs of fullerenes.
-polyhedra are also known as fullerene graphs since they correspond to the molecular graphs of fullerenes.
The 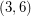 -polyhedra have precisely 4 triangular faces and they cover the complete graph
-polyhedra have precisely 4 triangular faces and they cover the complete graph 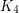 . Therefore, the eigenvalues
. Therefore, the eigenvalues  ,
, 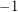 ,
, 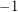 ,
, 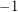 of
of 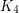 are also eigenvalues of every
are also eigenvalues of every 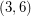 -polyhedron. Patrick Fowler computed eigenvalues of numerous examples and observed that all other eigenvalues occur in pairs of opposite values
-polyhedron. Patrick Fowler computed eigenvalues of numerous examples and observed that all other eigenvalues occur in pairs of opposite values  ,
,  , a similar phenomenon as for bipartite graphs. From the spectral information, the
, a similar phenomenon as for bipartite graphs. From the spectral information, the 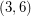 -polyhedra therefore behave like a combination of
-polyhedra therefore behave like a combination of 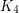 and a bipartite graph.
and a bipartite graph.
Horst Sachs and Peter John (private communication) found some reduction procedures which allow Fowler's Conjecture to be proved for many infinite classes of (3,6)-polyhedra.
Bibliography
[FJS] P. W. Fowler, P. E. John, H. Sachs, (3,6)-cages, hexagonal toroidal cages, and their spectra, Discrete mathematical chemistry (New Brunswick, NJ, 1998), pp. 139-174, DIMACS Ser. Discrete Math. Theoret. Comput. Sci. 51, Amer. Math. Soc., Providence, RI, 2000. MathSciNet
[M] B. Mohar: Problem of the Month
* indicates original appearance(s) of problem.
Link to preprint
You can find the proof on the arxiv:
Matt DeVos, Luis Goddyn, Bojan Mohar, Robert Samal: Cayley sum graphs and eigenvalues of 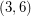 -fullerenes
-fullerenes
Robert Samal
Coming Soon
The proof is solid, but the paper is still in preliminary form.. coming soon!

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Is it done?
What is the status of your possible proof?
Gordon Royle