 login/create account
login/create account
Finite entailment of Positive Horn logic
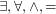 . Does the fragment
. Does the fragment 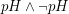 have the finite model property?
have the finite model property?
It doesn't really matter whether or not equality is allowed, as it may mostly be propagated out by substitution. The question is whether there an infinity axiom of the form 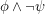 , for
, for 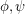 in pH?
in pH?
In [CMM08] it is proved that entailment of pH sentences is decidable. I.e. input, 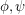 in pH and return yes if
in pH and return yes if 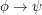 is true on all models. The question is whether this is the same as asking if entailment of pH is equivalent to finite entailment, i.e. if
is true on all models. The question is whether this is the same as asking if entailment of pH is equivalent to finite entailment, i.e. if 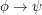 is true on all models iff it is true on all finite models.
is true on all models iff it is true on all finite models.
For the positive equality-free fragment of FO (bigger than pH), finite entailment and general entailment do not coincide, and the latter problem is undecidable. For existential positive logic, (smaller than pH), finite entailment and general entailment do coincide, and of course both are decidable. At present, the question as to whether finite entailment of pH is decidable is also open.
Bibliography
[CMM08] Hubie Chen, Florent R. Madelaine, Barnaby Martin: Quantified Constraints and Containment Problems. LICS 2008: 317-328
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Solved.
Solved in LICS 2017 "Herbrand Property, Finite Quasi-Herbrand Models, and a Chandra-Merlin Theorem for Quantified Conjunctive Queries"