 login/create account
login/create account
Covering systems with big moduli
Problem Does for every integer 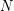 exist a covering system with all moduli distinct and at least equal to~
exist a covering system with all moduli distinct and at least equal to~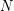 ?
?
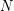 exist a covering system with all moduli distinct and at least equal to~
exist a covering system with all moduli distinct and at least equal to~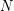 ?
? Let 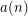 denote the residue class
denote the residue class 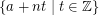 . A covering system (defined by Paul Erdos in early 1930's) is a finite collection
. A covering system (defined by Paul Erdos in early 1930's) is a finite collection 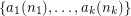 of residue classes whose union covers all the integers.
of residue classes whose union covers all the integers.
Such systems are easy to find if the moduli are allowed to repeat. They are known for many lower bounds 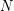 on the size of moduli: e.g.
on the size of moduli: e.g. 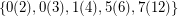 is such system for
is such system for 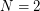 . Choi proved that it is possible to give an example for N = 20.
. Choi proved that it is possible to give an example for N = 20.
On the other hand, recently it was shown [FFKPY] that if such systems exist for arbitrary large 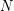 , then
, then 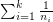 is not bounded.
is not bounded.
Bibliography
[FFKPY] Michael Filaseta, Kevin Ford, Sergei Konyagin, Carl Pomerance, Gang Yu: Sieving by large integers and covering systems of congruences, J. Amer. Math. Soc. 20 (2007), 495-517.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University