 login/create account
login/create account
A discrete iteration related to Pierce expansions
Conjecture Let 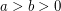 be integers. Set
be integers. Set 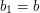 and
and 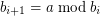 for
for 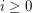 . Eventually we have
. Eventually we have 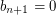 ; put
; put 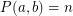 .
.
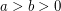 be integers. Set
be integers. Set 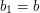 and
and 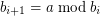 for
for 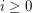 . Eventually we have
. Eventually we have 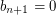 ; put
; put 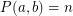 .
.
Example: 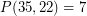 , since
, since 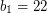 ,
, 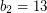 ,
, 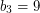 ,
, 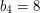 ,
, 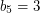 ,
, 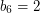 ,
, 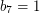 ,
, 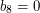 .
.
Prove or disprove: 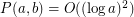 .
.
The best upper bound is currently 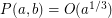 . For more information, see [ES].
. For more information, see [ES].
Bibliography
[ES] P. Erd\"os and J. Shallit, ``New bounds on the length of finite Pierce and Engel series'', S\'eminaire de Th\'eorie des Nombres de Bordeaux 3 (1991), 43--53.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
A different upper bound
This paper shows an upper bound of![$ O(\sqrt[3]a \sqrt[3]{\log(a)}) $](/files/tex/3e490226bc7f29b7c6a8e398ec9247b7ea735862.png) .
.
Edit: But looking at the title page of the paper, I see you already knew that ;)