 login/create account
login/create account
Fowler's Conjecture on eigenvalues of (3,6)-polyhedra ★★
Author(s): Fowler
Conjecture Let  be the graph of a
be the graph of a 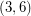 -polyhedron with
-polyhedron with 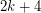 vertices. Then the eigenvalues of
vertices. Then the eigenvalues of  can be partitioned into three classes:
can be partitioned into three classes: 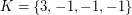 ,
, 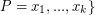 (where
(where 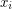 is nonnegative for
is nonnegative for 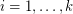 ), and
), and 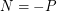 .
.
 be the graph of a
be the graph of a 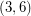 -polyhedron with
-polyhedron with 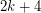 vertices. Then the eigenvalues of
vertices. Then the eigenvalues of  can be partitioned into three classes:
can be partitioned into three classes: 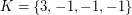 ,
, 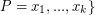 (where
(where 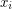 is nonnegative for
is nonnegative for 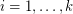 ), and
), and 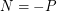 .
. Keywords: (3,6)-polyhedron; eigenvalues
Greenthumb guide
Use the Comments link in the Greenthumb menu to delete any unwanted comments. For an open problem submission which is not up to par, go to the comments section and then either demote it to the second tier by "unpublishing", or if it is truly worthless, delete. Please be very careful when doing so!
- Adding a category
- Keep the Title short
- The Body should generally be left empty
- no need to touch Input format
- for Category information, the only fields which need be touched are Container and Parent.
- set Comment settings to "disabled".
- Menu settings

 be a convex
be a convex  -
-
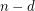 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University