I believe that Robert Samal has conjectured a version of this for the Lovasz function, i.e. that where . I can't find it in the Garden, but it is in this presentation by Samal: http://iuuk.mff.cuni.cz/research/cmi/cmi-I-Samal.pdf
login/create account
Drupal
CSI of Charles University
Lovasz Theta
I believe that Robert Samal has conjectured a version of this for the Lovasz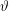
function, i.e. that ![\[\bar{\vartheta}(G \times H) = \min\{\bar{\vartheta}(G), \bar{\vartheta}(H)\}\]](/files/tex/a0db5601e339f9aac78ebd7894226f11e3c23260.png)
where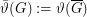 
. I can't find it in the Garden, but it is in this presentation by Samal: http://iuuk.mff.cuni.cz/research/cmi/cmi-I-Samal.pdf