Home » Subject » Combinatorics
Importance: Medium ✭✭
Author(s):
Subject: Combinatorics
Keywords:
Recomm. for undergrads: yes
Posted by: arbitrary
on: March 16th, 2008

Problem

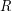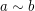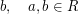Consider the finite set $ [n]=\{1,\dots,n\} $. We define a binary relation $ R $ over the set $ [n] $ and we write $ a\sim b $ to indicate $ a $ is related to $ b,\quad a,b\in R $. We have the following properties of $ R $:

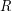(i) 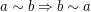$ a\sim b \Rightarrow b\sim a $

(ii)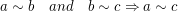$ a\sim b \quad and \quad b\sim c \Rightarrow a\sim c $

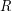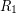A relation $ R $ together with a set $ [n] $ is a set of unordered pairs denoted by $ ([n],R) $. Consider the example $ ([n],R_1)=\{(1,2),(2,3),(4,12),(6,7)\} $. This is extendable to $ ([n],R_2)=\{(1,2),(2,3),(1,3),(4,12),(6,7)\} $. In this case we call $ R_1 $ to be equivalent to 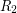$ R_2 $ (over $ [n] $).(This defines a equivalence relation over the set of relations) Two relations are called distinct if they are not equivalent.

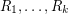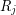Let $ R_1,\dots,R_k $ be all the equivalent relations. A set $ ([n],R_i) \quad \forall 1\leq i\leq k $ is said to be a minimal relation iff there does not exist a relation $ R_j $ which is extendable to $ R_i $.

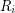1.Do all minimum relations among 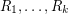$ R_1,\dots,R_k $ have same cardinality ie., same number of pairs?

2.Find the number of distinct relations

(i) when points are numbered

(ii) Upto isomorphism.

ps: I am a newcomer to this garden and newcomer to research too. Admin please move to relevant section if problem is not appropriate for this section.


Bibliography



* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options