 login/create account
login/create account
Problem Let  be a graph,
be a graph,  a countable end of
a countable end of  , and
, and 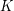 an infinite set of pairwise disjoint
an infinite set of pairwise disjoint  -rays in
-rays in  . Prove that there is a set
. Prove that there is a set 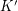 of pairwise disjoint
of pairwise disjoint  -rays that devours
-rays that devours  such that the set of starting vertices of rays in
such that the set of starting vertices of rays in 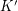 equals the set of starting vertices of rays in
equals the set of starting vertices of rays in 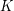 .
.
 be a graph,
be a graph,  a countable end of
a countable end of  , and
, and 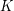 an infinite set of pairwise disjoint
an infinite set of pairwise disjoint  -rays in
-rays in  . Prove that there is a set
. Prove that there is a set 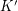 of pairwise disjoint
of pairwise disjoint  -rays that devours
-rays that devours  such that the set of starting vertices of rays in
such that the set of starting vertices of rays in 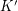 equals the set of starting vertices of rays in
equals the set of starting vertices of rays in 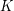 .
.
We say that a set of rays 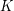 devours the end
devours the end  if every ray in
if every ray in  meets some ray in
meets some ray in 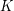 . An end is countable if there is a countable set of rays devouring it.
. An end is countable if there is a countable set of rays devouring it.
If 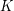 is a finite set of rays then it is not hard to prove (see [G]) that this problem has a positive answer:
is a finite set of rays then it is not hard to prove (see [G]) that this problem has a positive answer:
Theorem For every graph  and every countable end
and every countable end  of
of  , if
, if  has a set
has a set 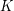 of
of 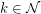 pairwise disjoint
pairwise disjoint  -rays, then it also has a set
-rays, then it also has a set 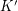 of
of  pairwise disjoint
pairwise disjoint  -rays that devours
-rays that devours  . Moreover,
. Moreover, 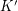 can be chosen so that its rays have the same starting vertices as the rays in~
can be chosen so that its rays have the same starting vertices as the rays in~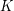 .
.
 and every countable end
and every countable end  of
of  , if
, if  has a set
has a set 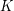 of
of 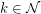 pairwise disjoint
pairwise disjoint  -rays, then it also has a set
-rays, then it also has a set 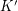 of
of  pairwise disjoint
pairwise disjoint  -rays that devours
-rays that devours  . Moreover,
. Moreover, 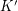 can be chosen so that its rays have the same starting vertices as the rays in~
can be chosen so that its rays have the same starting vertices as the rays in~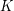 .
. Bibliography
*[G] A. Georgakopoulos, Infinite Hamilton Cycles in Squares of Locally Finite Graphs, Preprint.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University