I believe that this conjecture is true, and that it can be proved with standard tools. I will sketch the argument here. I certainly wouldn't claim this is a particularly great proof.. it's just the one my nose lead me to first. The main tools I need are as follows.
Theorem (Tutte) If does not have a perfect matching, then there exists a subset of vertices so that has more than components which have an odd number of vertices.
Corollary If is a connected bridgeless cubic graph, then for every edge , there exist perfect matchings so that and .
Now, let be a connected bridgeless cubic graph with the property that every 2-factor of is a (disjoint) union of cycles of length 5. Using the corollary (carefully), you can show the following in order:
\item does not have a cycle of length 2. \item does not have two triangles which share an edge. \item does not have a square and a triangle which share an edge. \item does not have a triangle. \item does not have a square.
Thus, must have girth 5. Next we will show that is 3-edge connected using the same corollary. Suppose (for a contradiction) that is only 2-edge-connected, and let be two edges which form a 2-edge cut so that and are in the same component of . Now, there must exist a perfect matching not using , so the complementary 2-factor must contain a 5-cycle which uses both the edges and . It follows that either is an edge or is an edge, and we may assume the latter without loss. Let be the neighbor of other than and let be the neighbor of other than . Now, there exists a perfect matching containing the edge , and the complementary 2-factor must contain a 5-cycle which uses all of the edges . It follows that either or , but either of these contradicts the fact that is bridgeless. This contradiction shows that is 3-edge connected. By a similar argument, you can prove that every 3-edge cut of consists of 3 edges incident with a common vertex. So, is cyclically 4-edge connected.
Next we establish that has property (*) which is a strengthening of what appears in the corollary.
(*) If and , then there is a perfect matching containing both and .
Suppose (for a contradiction) that (*) does not hold. Then has no perfect matching, so by Tutte's theorem there exists a subset of vertices so that has more than odd components. Let be the set of isolated vertices in , let be the set of odd components of with size , and let be the set of even components of . We know that by assumption, but in fact since must be an even number (as is even). Now, let and let be the edge cut in which separates from the rest of the vertices (). It follows from our construction that since every vertex in can contribute at most 3 edges to , and there are at most 6 edges in with one of as endpoint. On the other hand, since is cyclically 4-edge connected, every component in must contribute at least 4 edges to , and every vertex in contributes exactly 3 edges to , so . It follows from this that , and that every vertex in must have all three incident edges in . Thus, is a bipartite graph. Now, there exists a perfect matching of which contains the edge , and every odd cycle in the complementary 2-factor must contain either or , so the complementary 2-factor cannot have 2 odd cycles - giving us a contradiction.
With property (*) in hand, we are ready to complete the proof. Property (*) implies that every 3-edge path must be contained in a cycle of length 5, and it follows from this that every 2-edge path of is contained in at least two 5-cycles. Let be a vertex of , let be the neighbors of , and assume that the neighbors of are , , and (respectively). It follows from the fact that has girth 5 that all of these vertices we have named are distinct. Since the 2-edge path with edges is contained in two cycles of length 5, there must be edges between and . Similarly, there are edges between and , and between and . It follows from this that , and with a little more work using the girth assumption, it can be shown that is isomorphic to Petersen as required.
not too hard
I believe that this conjecture is true, and that it can be proved with standard tools. I will sketch the argument here. I certainly wouldn't claim this is a particularly great proof.. it's just the one my nose lead me to first. The main tools I need are as follows.
Now, let be a connected bridgeless cubic graph with the property that every 2-factor of
be a connected bridgeless cubic graph with the property that every 2-factor of  is a (disjoint) union of cycles of length 5. Using the corollary (carefully), you can show the following in order:
is a (disjoint) union of cycles of length 5. Using the corollary (carefully), you can show the following in order:
\item does not have a cycle of length 2. \item
does not have a cycle of length 2. \item  does not have two triangles which share an edge. \item
does not have two triangles which share an edge. \item  does not have a square and a triangle which share an edge. \item
does not have a square and a triangle which share an edge. \item  does not have a triangle. \item
does not have a triangle. \item  does not have a square.
does not have a square.
Thus, must have girth 5. Next we will show that
must have girth 5. Next we will show that  is 3-edge connected using the same corollary. Suppose (for a contradiction) that
is 3-edge connected using the same corollary. Suppose (for a contradiction) that  is only 2-edge-connected, and let
is only 2-edge-connected, and let 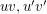 be two edges which form a 2-edge cut so that
be two edges which form a 2-edge cut so that  and
and 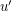 are in the same component of
are in the same component of 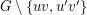 . Now, there must exist a perfect matching not using
. Now, there must exist a perfect matching not using 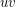 , so the complementary 2-factor must contain a 5-cycle which uses both the edges
, so the complementary 2-factor must contain a 5-cycle which uses both the edges 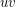 and
and 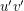 . It follows that either
. It follows that either 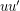 is an edge or
is an edge or 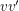 is an edge, and we may assume the latter without loss. Let
is an edge, and we may assume the latter without loss. Let  be the neighbor of
be the neighbor of  other than
other than 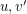 and let
and let 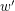 be the neighbor of
be the neighbor of 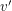 other than
other than 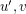 . Now, there exists a perfect matching containing the edge
. Now, there exists a perfect matching containing the edge 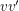 , and the complementary 2-factor must contain a 5-cycle which uses all of the edges
, and the complementary 2-factor must contain a 5-cycle which uses all of the edges 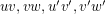 . It follows that either
. It follows that either 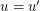 or
or 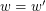 , but either of these contradicts the fact that
, but either of these contradicts the fact that  is bridgeless. This contradiction shows that
is bridgeless. This contradiction shows that  is 3-edge connected. By a similar argument, you can prove that every 3-edge cut of
is 3-edge connected. By a similar argument, you can prove that every 3-edge cut of  consists of 3 edges incident with a common vertex. So,
consists of 3 edges incident with a common vertex. So,  is cyclically 4-edge connected.
is cyclically 4-edge connected.
Next we establish that has property (*) which is a strengthening of what appears in the corollary.
has property (*) which is a strengthening of what appears in the corollary.
(*) If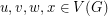 and
and 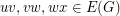 , then there is a perfect matching containing both
, then there is a perfect matching containing both 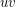 and
and 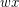 .
.
Suppose (for a contradiction) that (*) does not hold. Then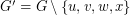 has no perfect matching, so by Tutte's theorem there exists a subset of vertices
has no perfect matching, so by Tutte's theorem there exists a subset of vertices 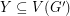 so that
so that  has more than
has more than  odd components. Let
odd components. Let 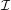 be the set of isolated vertices in
be the set of isolated vertices in  , let
, let 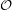 be the set of odd components of
be the set of odd components of  with size
with size 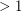 , and let
, and let 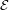 be the set of even components of
be the set of even components of  . We know that
. We know that 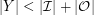 by assumption, but in fact
by assumption, but in fact  since
since 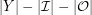 must be an even number (as
must be an even number (as 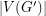 is even). Now, let
is even). Now, let 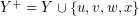 and let
and let  be the edge cut in
be the edge cut in  which separates
which separates 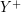 from the rest of the vertices (
from the rest of the vertices (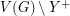 ). It follows from our construction that
). It follows from our construction that 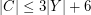 since every vertex in
since every vertex in 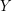 can contribute at most 3 edges to
can contribute at most 3 edges to  , and there are at most 6 edges in
, and there are at most 6 edges in  with one of
with one of 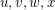 as endpoint. On the other hand, since
as endpoint. On the other hand, since  is cyclically 4-edge connected, every component in
is cyclically 4-edge connected, every component in 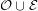 must contribute at least 4 edges to
must contribute at least 4 edges to  , and every vertex in
, and every vertex in 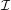 contributes exactly 3 edges to
contributes exactly 3 edges to  , so
, so 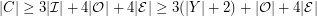 . It follows from this that
. It follows from this that 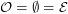 , and that every vertex in
, and that every vertex in 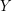 must have all three incident edges in
must have all three incident edges in  . Thus,
. Thus, 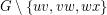 is a bipartite graph. Now, there exists a perfect matching of
is a bipartite graph. Now, there exists a perfect matching of  which contains the edge
which contains the edge 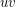 , and every odd cycle in the complementary 2-factor must contain either
, and every odd cycle in the complementary 2-factor must contain either  or
or 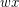 , so the complementary 2-factor cannot have 2 odd cycles - giving us a contradiction.
, so the complementary 2-factor cannot have 2 odd cycles - giving us a contradiction.
With property (*) in hand, we are ready to complete the proof. Property (*) implies that every 3-edge path must be contained in a cycle of length 5, and it follows from this that every 2-edge path of is contained in at least two 5-cycles. Let
is contained in at least two 5-cycles. Let  be a vertex of
be a vertex of  , let
, let 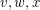 be the neighbors of
be the neighbors of  , and assume that the neighbors of
, and assume that the neighbors of 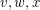 are
are 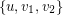 ,
, 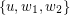 , and
, and 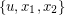 (respectively). It follows from the fact that
(respectively). It follows from the fact that  has girth 5 that all of these vertices we have named are distinct. Since the 2-edge path with edges
has girth 5 that all of these vertices we have named are distinct. Since the 2-edge path with edges 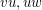 is contained in two cycles of length 5, there must be
is contained in two cycles of length 5, there must be 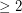 edges between
edges between 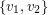 and
and 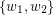 . Similarly, there are
. Similarly, there are 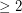 edges between
edges between 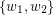 and
and 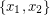 , and between
, and between 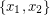 and
and 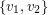 . It follows from this that
. It follows from this that 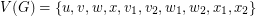 , and with a little more work using the girth assumption, it can be shown that
, and with a little more work using the girth assumption, it can be shown that  is isomorphic to Petersen as required.
is isomorphic to Petersen as required.