 login/create account
login/create account
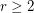 be an integer and let
be an integer and let  be a minor minimal clutter with
be a minor minimal clutter with 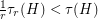 . Then either
. Then either  has a
has a 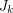 minor for some
minor for some 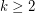 or
or  has Lehman's property.
has Lehman's property. See Wikipedia's Clutter for definitions of clutter and clutter minors. The clutter 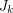 is the degenerate projective plane with vertex set
is the degenerate projective plane with vertex set 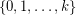 and edge set
and edge set 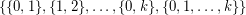 . If
. If 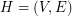 is a clutter, then for every positive integer
is a clutter, then for every positive integer  we let
we let 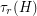 denote the largest multiset of vertices of
denote the largest multiset of vertices of  which hit every edge at least
which hit every edge at least  times. Note that
times. Note that 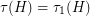 and that
and that 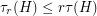 .
.
We say that a clutter  with
with 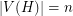 ,
, 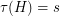 and
and 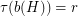 has Lehman's property if
has Lehman's property if 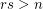 ,
, 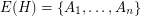 ,
, 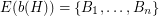 , and the following properties are satisfied.
, and the following properties are satisfied.
- \item
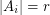 for every
for every 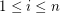 . \item
. \item 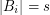 for every
for every 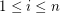 . \item
. \item 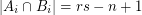 for
for 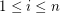 \item
\item 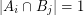 if
if 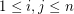 and
and 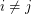 . \item every
. \item every 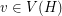 lies in exactly
lies in exactly  edges of
edges of  ,
,  edges of
edges of 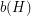 , and
, and 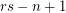 members of
members of 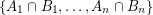 .
. Although the conditions in Lehman's condition are extremely stringent, Lehman [L] showed that every minor minimal clutter with the MFMC property satisfies these properties. Since the MFMC property for  implies
implies 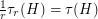 (and the degenerate projective planes are minor minimal without MFMC), if true, the above conjecture would be a nice extension of Lehman's theorem.
(and the degenerate projective planes are minor minimal without MFMC), if true, the above conjecture would be a nice extension of Lehman's theorem.
Ding [D] proved this conjecture for 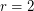 , but it is open for all other cases.
, but it is open for all other cases.
Bibliography
*[D] G. Ding, Clutters with tau_2=2 tau, Discrete Math. 115 (1993), no. 1-3, 141--152. MathSciNet.
[L] A. Lehman, On the width-length inequality, mimeographic notes, published 1979. Math. Program. 17, 403--417 MathSciNet.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University