Home » Subject » Combinatorics
Importance: Medium ✭✭
Author(s): Davis, James A.
Entringer, Roger C.
Graham, Ronald L.
Simmons, Gustavus J.
Subject: Combinatorics
Keywords: monotone arithmetic progression
permutation
Recomm. for undergrads: no
Posted by: vjungic
on: October 3rd, 2007
Question   Is it true that every permutation of positive integers must contain monotone 4-term arithmetic progressions?

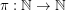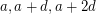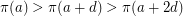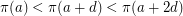It is not difficult to see that any permutation of positive integers contains a monotone 3-term arithmetic progression, i.e., that for any permutation $ \pi :\mathbb{N}\to \mathbb{N} $ there is a 3-term arithmetic progression $ a, a+d, a+2d $ such that $ \pi (a)>\pi (a+d)>\pi (a+2d) $ or $ \pi (a)<\pi (a+d)<\pi (a+2d) $.

In [DEGS] an example of a permutation of 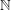$ \mathbb{N} $ that does not contain a monotone 5-term arithmetic progression is given.

Bibliography

*[DEGS] J. A. Davis, R. C. Entringer, R. L. Graham, and G. J. Simmons, On permutations containing no long arithmetic progression, Acta Arithmetica XXXIV.1 (1977), 81-90.

[LR] Bruce M. Landman and Aaron Robertson, Ramsey Theory on the Integers, Stud. Math. Libr. 24, AMS Providence, RI, 2004.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options