Home » Subject » Geometry
Importance: Medium ✭✭
Author(s): Deza, Antoine
Terlaky, Tamas
Zinchenko, Yuriy
Subject: Geometry
Keywords: arrangement
diameter
polytope
Recomm. for undergrads: no
Posted by: deza
on: September 30th, 2007
Conjecture   The average diameter of a bounded cell of a simple arrangement defined by $ n $ hyperplanes in dimension $ d $ is not greater than $ d $.

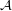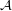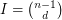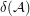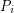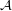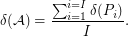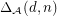Let $ \mathcal{A} $ be a simple arrangement formed by $ n $ hyperplanes in dimension $ d $. The number of bounded cells of $ \mathcal{A} $ is $ I={n-1\choose d} $. Let $ \delta(\mathcal{A}) $ denote the average diameter of a bounded cell $ P_i $ of $ \mathcal{A} $; that is, $$ \delta(\mathcal{A})=\frac{\sum_{i=1}^{i=I}\delta(P_i)}{I}. $$ Let $ \Delta_{\mathcal{A}}({d,n}) $ denote the largest possible average diameter of a bounded cell of a simple arrangement defined by $ n $ inequalities in dimension $ d $.

We have [DTZ,DX]:

If the conjecture of Hirsch holds, then 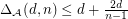$ \Delta_{\mathcal{A}}(d,n)\leq d+\frac{2d}{n-1} $.

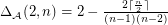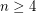$ \Delta_{\mathcal{A}}({2,n})=2-\frac{2\lceil\frac{n}{2}\rceil}{(n-1)(n-2)} $ for $ n\geq 4 $.

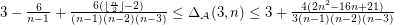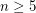$ 3-\frac{6}{n-1}+\frac{6(\lfloor\frac{n}{2}\rfloor-2)}{(n-1)(n-2)(n-3)}\leq \Delta_{{\mathcal A}}(3,n)\leq 3 + \frac{4(2n^2-16n+21)}{3(n-1)(n-2)(n-3)} $ for $ n\geq 5 $.

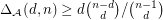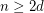$ \Delta_{{\mathcal A}}(d,n)\geq d{n-d \choose d}/{n-1 \choose d} $ for $ n\geq 2d $.

Related problems

Hirsch Conjecture

Bibliography

*[DTZ] A. Deza, T. Terlaky and Y. Zinchenko: Polytopes and arrangements : diameter and curvature. Operations Research Letters (to appear).

[DX] A. Deza and F. Xie: Hyperplane arrangements with large average diameter. Centre de Recherches Mathematiques and American Mathematical Society series (to appear).


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options