Home » Subject » Graph Theory
Importance: Medium ✭✭
Author(s):
Subject: Graph Theory
Keywords:
Recomm. for undergrads: no
Posted by: Iradmusa
on: April 20th, 2023

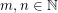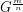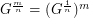Let $ G $ be a graph and $ m,n\in \mathbb{N} $. The graph $ G^{\frac{m}{n}} $ is defined to be the $ m $-power of the $ n $-subdivision of $ G $. In other words, $ G^{\frac{m}{n}}=(G^{\frac{1}{n}})^m $.

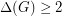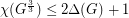Conjecture   Let $ G $ be a graph with $ \Delta(G)\geq 2 $. Then $ \chi(G^{\frac{3}{3}})\leq 2\Delta(G)+1 $.

Bibliography

[1] Mahsa Mozafari-Nia and M. N. Iradmusa, Simultaneous coloring of vertices and incidences of graphs, Australasian Journal of Combinatorics, Vol. 85, Mo. 3, pp. 287-307, 2023.

[2] Mahsa Mozafari-Nia and M. N. Iradmusa, Simultaneous coloring of vertices and incidences of outerplanar graphs, Electronic Journal of Graph Theory and Applications, Vol.11, No.1, pp.245-262, 2023.

[3] Mahsa Mozafari-Nia and M. N. Iradmusa, A note on coloring of 3/3-power of subquartic graphs, Australasian Journal of Combinatorics, Vol. 79, No. 3, pp. 454-460, 2021.

[4] M. N. Iradmusa, A short proof of 7-colorability of 3/3-power of subcubic graphs, Iranian Journal of Science and Technology, Transactions A: Science, Vol. 44, No. 1, pp. 225-226, 2020.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options