 login/create account
login/create account
Conjecture For any bipartite graph  and graph
and graph  , the number of homomorphisms from
, the number of homomorphisms from  to
to  is at least
is at least 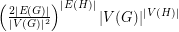 .
.
 and graph
and graph  , the number of homomorphisms from
, the number of homomorphisms from  to
to  is at least
is at least 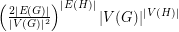 .
.
A homomorphism from a graph  to a graph
to a graph  is a mapping
is a mapping 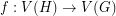 which preserves edges. Given graphs
which preserves edges. Given graphs  and
and  , the homomorphism density of
, the homomorphism density of  in
in  , denoted
, denoted 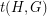 , is the probability that a random function
, is the probability that a random function 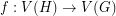 is a homomorphism. That is,
is a homomorphism. That is,
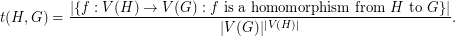
In this language, Sidorenko's Conjecture says that, if  is bipartite, then every graph
is bipartite, then every graph  satisfies
satisfies
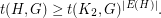
There are lots of results on Sidorenko's Conjecture; rather than listing them all here, we encourage the reader to see the references of the recent paper [CL].
Bibliography
[CL] David Conlon and Joonkyung Lee: Sidorenko's conjecture for blow-ups, submitted.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University