 login/create account
login/create account
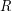 (first time when the players occupy the same point) which can be achieved assuming the two players must adopt the same strategy?
(first time when the players occupy the same point) which can be achieved assuming the two players must adopt the same strategy? This is one of a handful of rendezvous problems where two players must find one another in a certain structured domain. See [AG2] for a thorough development of this subject. This is a symmetric rendezvous problem since each player is forced to adopt the same strategy. If we drop this constraint, Alpern and Gal [AG] have shown that the inf expected meeting time is 3.25.
Han, Du, Vera, and Zuluaga [HDVZ] have shown that strategies in which the players move at maximum speed and only change direction at integer times dominate among all possible strategies - thus reducing this problem to a discrete one. These same authors improve upon a series of results by tightening the upper and lower bounds, proving 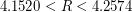 . Further, they conjecture
. Further, they conjecture 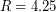 .
.
Bibliography
*[A] S. Alpern, The rendezvous search problem. SIAM J. Control Optim. 33 (1995), no. 3, 673--683 MathSciNet
[AG1] S. Alpern and S. Gal, Rendezvous search on the line with distinguishable players. SIAM J. Control Optim. 33 (1995), no. 4, 1270--1276. MathSciNet
[AG2] S. Alpern and S. Gal, The theory of search games and rendezvous. International Series in Operations Research & Management Science, 55. Kluwer Academic Publishers, Boston, MA, 2003. MathSciNet
[HDVZ] Q. Han, D. Du, J. C. Vera, and L. F. Zuluaga, Improved bounds for the symmetric rendezvous search problem on the line
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University