Unless I am mistaken, it appears that there does not exist any for which any of the above problems has a positive solution. For instance, let be the complete graph with vertex set , and define to be the edge-cut of consisting of all edges between and . Now define a weighting of by assigning each edge in weight 1 and every other edge weight 2. So, the subgraph (consisting of all edges of weight 1) is isomorphic to - and since has edge-disjoint spanning trees (by the Nash-Williams theorem, say), our procedure may well choose trees so that all of the edges in all of these graphs are in . But then will not have a Hamiltonian path since it is a subgraph of .
Of course, we may modify the edge weights here so that the procedure is forced to choose so that all of these trees have their edges in .
Is this statement correct?
Unless I am mistaken, it appears that there does not exist any for which any of the above problems has a positive solution. For instance, let
for which any of the above problems has a positive solution. For instance, let  be the complete graph with vertex set
be the complete graph with vertex set 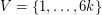 , and define
, and define  to be the edge-cut of
to be the edge-cut of  consisting of all edges between
consisting of all edges between 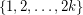 and
and 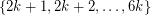 . Now define a weighting of
. Now define a weighting of  by assigning each edge in
by assigning each edge in  weight 1 and every other edge weight 2. So, the subgraph
weight 1 and every other edge weight 2. So, the subgraph 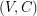 (consisting of all edges of weight 1) is isomorphic to
(consisting of all edges of weight 1) is isomorphic to 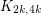 - and since
- and since 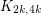 has
has  edge-disjoint spanning trees (by the Nash-Williams theorem, say), our procedure may well choose trees
edge-disjoint spanning trees (by the Nash-Williams theorem, say), our procedure may well choose trees 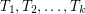 so that all of the edges in all of these graphs are in
so that all of the edges in all of these graphs are in  . But then
. But then 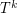 will not have a Hamiltonian path since it is a subgraph of
will not have a Hamiltonian path since it is a subgraph of 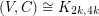 .
.
Of course, we may modify the edge weights here so that the procedure is forced to choose so that all of these trees have their edges in
so that all of these trees have their edges in  .
.