Home ยป Difference between neighbors in a matrix

Related questions: continued

On July 6th, 2013 Vadim Lioubimov says:

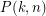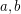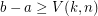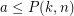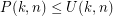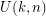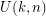2. What is the smallest number, denoted $ P(k,n) $, to guarantee that a $ [k]^n $-matrix $ A $ with the entries $ [k^n] $ has 2 neighboring entries $ a,b $ such that $ b-a\ge V(k,n) $ and $ a \le P(k,n) $? Obviously, $ P(k,n)\le U(k,n) $, where $ U(k,n) $ is the smallest number such that any subset of $ [k]^n $ of size $ U(k,n) $ has at least 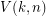$ V(k,n) $ neighbors. 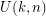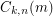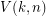Due to Theorem 11, $ U(k,n) $ is the smallest number $ m $ such that the initial segment $ C_{k,n}(m) $ of length $ m $ in the simplicial order on $ [k]^n $ has $ V(k,n) $ neighbors. In your proof you used the fact that 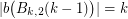$ |b\big(B_{k,2}(k-1)\big)| = k $, which implies by Theorem 11 that 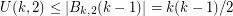$ U(k,2)\le |B_{k,2}(k-1)| = k(k-1)/2 $. However this bound is not tight. Consider the hamming ball 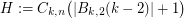$ H:=C_{k,n}\big(|B_{k,2}(k-2)|+1\big) $. 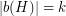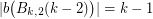It is easy to see that $ |b(H)| = k $ and $ |b\big(B_{k,2}(k-2)\big)| = k-1 $. 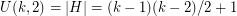Thus $ U(k,2)= |H| = (k-1)(k-2)/2 +1 $. What about higher dimensions?

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options