 login/create account
login/create account
Problem Can 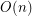 -size circuits compute the function
-size circuits compute the function  on
on 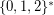 defined inductively by
defined inductively by 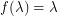 ,
, 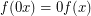 ,
, 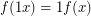 , and
, and 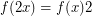 ?
?
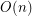 -size circuits compute the function
-size circuits compute the function  on
on 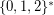 defined inductively by
defined inductively by 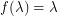 ,
, 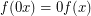 ,
, 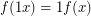 , and
, and 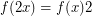 ?
?
This function moves all 2s in  flush-right, leaving the sequence of 0s and 1s the same, and represents stable topological sort of the partial order
flush-right, leaving the sequence of 0s and 1s the same, and represents stable topological sort of the partial order 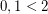 . It is linear-time computable in any model that supports the operations of a double-ended queue in
. It is linear-time computable in any model that supports the operations of a double-ended queue in 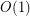 time, including multi-tape Turing machines, but is to me the "easiest" function for which I do not know linear-size circuits. By contrast sorting
time, including multi-tape Turing machines, but is to me the "easiest" function for which I do not know linear-size circuits. By contrast sorting 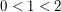 , called the "Dutch National Flag Problem", has
, called the "Dutch National Flag Problem", has 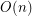 -size circuits by counting. It suffices to compute
-size circuits by counting. It suffices to compute 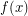 when
when  is a power of
is a power of  and exactly half the entries are
and exactly half the entries are  . For this and more see my Computational Complexity blog item, PDF file here.
. For this and more see my Computational Complexity blog item, PDF file here.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University