 login/create account
login/create account
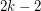 contains every oriented tree of order
contains every oriented tree of order  as a subdigraph.
as a subdigraph. The conjectured bound is best possible, because a regular tournament of order 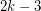 does not contain the oriented tree consisting of a vertex dominating
does not contain the oriented tree consisting of a vertex dominating 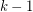 leaves.
leaves.
Let  be the function
be the function  such that every oriented tree of order
such that every oriented tree of order  is
is 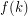 -universal, that is contained in every digraph with chromatic number at least
-universal, that is contained in every digraph with chromatic number at least 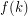 . Burr proved that
. Burr proved that 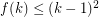 . This was slightly improved by Addario-Berry et al. [AHL+] who proved
. This was slightly improved by Addario-Berry et al. [AHL+] who proved 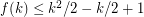 .
.
Burr's conjecture has been proved only in few particular cases of digraphs: tournaments, and acyclic digraphs. Kühn, Mycroft, and Osthus [KMS] showed that every oriented tree of order  is contained in every tournament of order
is contained in every tournament of order 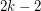 for all sufficiently large
for all sufficiently large  (so proving a Conjecture of Sumner); Addario-Berry et al. [AHL+] proved that every acyclic digraph with chromatic number
(so proving a Conjecture of Sumner); Addario-Berry et al. [AHL+] proved that every acyclic digraph with chromatic number  contains every oriented tree of order
contains every oriented tree of order  .
.
Burr's conjecture or some approximation have been also proved for special classes of trees. Gallai-Roy's celebrated theorem states that every directed path of order  is
is  -universal; El-Sahili [E] proved that every oriented path of order
-universal; El-Sahili [E] proved that every oriented path of order 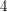 is
is 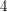 -universal and that the antidirected path of order
-universal and that the antidirected path of order  is
is  -universal; Addario-Berry, Havet, and Thomassé [AHT] showed that every oriented path of order
-universal; Addario-Berry, Havet, and Thomassé [AHT] showed that every oriented path of order  whose vertex set can be partioned into two directed paths is
whose vertex set can be partioned into two directed paths is  -universal; Addario-Berry et al. [AHL+] showed that antidirected trees (oriented trees in which every vertex has in-degree
-universal; Addario-Berry et al. [AHL+] showed that antidirected trees (oriented trees in which every vertex has in-degree  or out-degree
or out-degree  ) are
) are 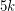 -universal.
-universal.
Havet, generalizing a conjecture of Havet and Thomassé (see [H]) on tournaments, conjectured that the following could also be true.
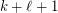 contains every oriented tree of order
contains every oriented tree of order  with
with  leaves.
leaves. Bibliography
[AHL+] L. Addario-Berry, F. Havet, C. Linhares Sales, B. Reed, and S. Thomassé. Oriented trees in digraphs. Discrete Mathematics, 313(8):967-974, 2013.
[AHT] L. Addario-Berry, F. Havet, and S. Thomassé, Paths with two blocks in  -chromatic digraphs, J. of Combinatorial Theory Ser. B, 97 (2007), 620--626.
-chromatic digraphs, J. of Combinatorial Theory Ser. B, 97 (2007), 620--626.
* [B] A. Burr, Subtrees of directed graphs and hypergraphs, Proceedings of the Eleventh Southeastern Conference on Combinatorics, Graph Theory and Computing, Boca Raton, Congr. Numer., 28 (1980), 227--239.
[H] F. Havet, Trees in tournaments. Discrete Mathematics 243 (2002), no. 1-3, 121--134.
[KOM] D. Kühn, D. Osthus, and R. Mycroft, A proof of Sumner's universal tournament conjecture for large tournaments, Proceedings of the London Mathematical Society 102 (2011), 731--766.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University