 login/create account
login/create account
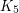 concentrated on a single value?
concentrated on a single value? Let  be a graph with vertex set
be a graph with vertex set 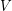 and edge set
and edge set  . An
. An 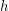 -lift
-lift  is a graph with vertex set
is a graph with vertex set 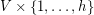 , such that
, such that 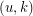 and
and 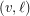 may only be adjacent in
may only be adjacent in  if
if 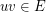 , and for each
, and for each 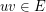 , the edges between
, the edges between 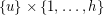 and
and 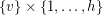 form a perfect matching.
form a perfect matching.
A random 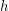 -lift of
-lift of  is a graph drawn uniformly at random from the set of all
is a graph drawn uniformly at random from the set of all 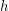 -lifts of
-lifts of  . This amounts to choosing, independently at random, a perfect matching for each edge of
. This amounts to choosing, independently at random, a perfect matching for each edge of  . One is generally interested in properties of random
. One is generally interested in properties of random 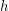 -lifts when
-lifts when 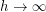 .
.
Amit, Linial, and Matousek [ALM02] have studied the chromatic number of random lifts. They ask whether a the chromatic number of a random 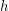 -lift of
-lift of 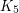 is asymptotically almost surely a single number.
is asymptotically almost surely a single number.
It is easy to see that this number may be either 3 or 4. Farzad and Theis [FT12] have shown that random lifts of 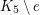 are asymptotically almost surely 3-colorable.
are asymptotically almost surely 3-colorable.
A more general question is this.
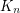 concentrated on a single value?
concentrated on a single value? Amit, Linial, and Matousek [ALM02] have shown that the chromatic number of a random lift of 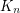 is in
is in 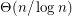 .
.
Bibliography
*[ALM02] Random Lifts of Graphs III: Independence and Chromatic Number, A. Amit, N. Linial and J. Matousek, Random Structures and Algorithms, 20(2002) 1-22.
[FT12] Random lifts of 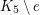 are 3-colourable. B. Farzad and D.O. Theis. SIAM J. Discrete Math. 26:1 (2012), 169–179.
are 3-colourable. B. Farzad and D.O. Theis. SIAM J. Discrete Math. 26:1 (2012), 169–179.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University