Open Problem Garden

Let be a finite undirected simple graph. A good edge labeling of is an assignment of distinct numbers to the edges such that every cycle has at least two local maxima. (The distinctness of the labels is required only to make the term `local maximum' unambiguous.)

Equivalently, a labeling of the edges is good, if for every pair of distinct vertices 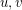, there is at most one increasing path from to .

It is easy to verify that the graphs 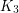and 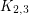have no good edge labeling. In [ACGH2] an infinite class of graphs without good edge labelings is given. All these graphs have many 4-cycles.

Indeed, no example is known of a graph of girth 5 or more without a good edge labeling. In other words, it may be possible that 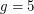suffices for the conjecture.