Home » Subject » Graph Theory » Coloring » Vertex coloring
Importance: Low ✭
Author(s): Heckman, Christopher C.
Thomas, Robin
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: fractional coloring
Recomm. for undergrads: no
Posted by: Andrew King
on: April 20th, 2011
Solved by: Zdeněk Dvořák, Jean-Sébastien Sereni, and Jan Volec [DSV]
Conjecture   Every triangle-free graph with maximum degree at most 3 has fractional chromatic number at most 14/5.

This conjecture was posed by Heckman and Thomas [HT]. Due to the generalized Petersen graph 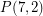$ P(7,2) $, which has 14 vertices and no stable set of size 6, this would be best possible.

The conjecture requires that every triangle-free subcubic graph contains a stable set of size at least 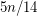$ 5n/14 $. This was first proved by Staton [S]. The proof was then improved Jones [J]. Griggs and Murphy [GM] gave a linear-time algorithm for finding a stable set of size at least 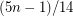$ (5n-1)/14 $ for any connected subcubic graph, and Heckman and Thomas [HT] have a linear-time algorithm to find a stable set of size at least $ 5n/14 $.

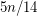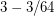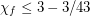Hatami and Zhu [HZ] proved that triangle-free subcubic graphs have fractional chromatic number at most $ 3-3/64 $. Lu and Peng [LP] improved this bound to $ \chi_f \leq 3- 3/43 $.

Bibliography

**[DSV] Z. Dvořák, J.-S. Sereni, and J. Volec, Subcubic triangle-free graphs have fractional chromatic number at most 14/5, arXiv:1301.5296 [math.CO]

[GM] J. Griggs and O. Murphy. Edge density and the independence ratio in triangle-free graphs with maximum degree three. Discrete Math. 152 (1996) 157--170.

[HZ] H. Hatami and X. Zhu. The fractional chromatic number of graphs of maximum degree at most three. SIAM J. Discrete Math. 233 (2001) 233-237.

*[HT] Christopher Carl Heckman and Robin Thomas. A new proof of the independence ratio of triangle-free cubic graphs. Discrete Math. 233 (2001), 233--237.

[J] K. F. Jones. Size and independence in triangle-free graphs with maximum degree three. J. Graph Theory 14 (1990) 525--535.

[LP] L. Lu and X. Peng. The fractional chromatic number of triangle-free graphs with 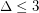$ \Delta \leq 3 $.

[S] W. Staton. SOme Ramsey-type numbers and the independence ratio. Trans. Amer. Math. Soc. 256 (1979) 353--370.


* indicates original appearance(s) of problem.
1 comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options