Now still needs to be covered twice, which cannot be done by 1 color as then again one needs 6 colors. One of the colors has to be color 2, otherwise this will leave towards and and therefore there will be no escape possibility from for the two new colors. So the triangle is colored with color 2. By symmetry the triangle is also one color cycle (color 4). Now , and are not colored and therefore need to be in the cycle of color 3 and the cycle of color 5. But then has degree 3 in both cycles which is a contradiction. So a 5-cycle double cover containing this cycle does not exist.
login/create account
Drupal
CSI of Charles University
Explanation of the 3-connected counterexample (Part II)
Now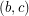
still needs to be covered twice, which cannot be done by 1 color as then again one needs 6 colors. One of the colors has to be color 2, otherwise this will leave 
towards 
and 
and therefore there will be no escape possibility from 
for the two new colors. So the triangle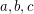 
is colored with color 2. By symmetry the triangle 
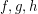is also one color cycle (color 4). Now 
, 
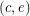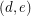and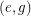 
are not colored and therefore need to be in the cycle of color 3 and the cycle of color 5. But then 
has degree 3 in both cycles which is a contradiction.
So a 5-cycle double cover containing this cycle does not exist.