Consider the circuit to be color 1, now on either side of the 2-cut, we need three more colors, of which only one color can serve both (due to the 2-cut), so we need at least 6 colors (6 cycles).
----------- It could be so that I am making a mistake, if so, please explain my mistake to me. I came to this point by simple trial and error. I would like to upload a simple picture, but I seem to be a little lost on how to do this.
?: Counterexample for a graph with a 2-cut
Adjacency matrix (in alphabetical order):
Consider the circuit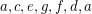 to be color 1, now on either side of the 2-cut, we need three more colors, of which only one color can serve both (due to the 2-cut), so we need at least 6 colors (6 cycles).
to be color 1, now on either side of the 2-cut, we need three more colors, of which only one color can serve both (due to the 2-cut), so we need at least 6 colors (6 cycles).
-----------
It could be so that I am making a mistake, if so, please explain my mistake to me.
I came to this point by simple trial and error.
I would like to upload a simple picture, but I seem to be a little lost on how to do this.
Nieke Aerts