 login/create account
login/create account
Problem Two players alternately write O's (first player) and X's (second player) in the unoccupied cells of an 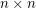 grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
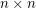 grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15. Bibliography
R. Bacher and S. Eliahou, "Extremal binary matrices without constant 2-squares," J. of Combinatorics, Volume 1, Number 1, 77-100, 2010.
* Erickson, Martin, "Pearls of Discrete Mathematics," CRC Press, 2010
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University