 login/create account
login/create account
Conjecture If in a bridgeless cubic graph  the cycles of any
the cycles of any  -factor are odd, then
-factor are odd, then 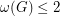 , where
, where 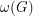 denotes the oddness of the graph
denotes the oddness of the graph  , that is, the minimum number of odd cycles in a
, that is, the minimum number of odd cycles in a  -factor of
-factor of  .
.
 the cycles of any
the cycles of any  -factor are odd, then
-factor are odd, then 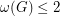 , where
, where 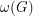 denotes the oddness of the graph
denotes the oddness of the graph  , that is, the minimum number of odd cycles in a
, that is, the minimum number of odd cycles in a  -factor of
-factor of  .
. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University