Home » Subject » Geometry
Importance: High ✭✭✭
Author(s):
Subject: Geometry
Keywords: arithmetic mean
geometric mean
Inequality
packing
Recomm. for undergrads: no
Posted by: mdevos
on: April 6th, 2009
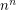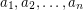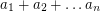Question   Is is possible to pack $ n^n $ rectangular $ n $-dimensional boxes each of which has side lengths $ a_1,a_2,\ldots,a_n $ inside an $ n $-dimensional cube with side length $ a_1 + a_2 + \ldots a_n $?

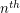Taking the arithmetic/geometric mean inequality \[ (a_1 a_2 \ldots a_n)^{1/n} \le \frac{a_1 + a_2 + \ldots a_n}{n} \] multiplying both sides by $ n $ and then raising both sides to the $ n^{th} $ power yields: \[ n^n \cdot a_1 a_2 \ldots a_n \le (a_1 + a_2 + \ldots a_n)^{n}.\] So, in the above question, the volume of the cube is at least the sum of the volumes of the rectangular boxes. Furthermore, a positive solution to this question would yield a strengthening of the arithmetic/geometric mean inequality.

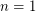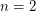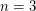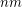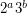For $ n=1 $ the problem is trivial, for $ n=2 $ it is immediate, and for $ n=3 $ it is tricky, but possible. It is also known that a solution for dimensions $ n $ and $ m $ can be combined to yield a solution for dimension $ nm $. Thus, the question has a positive answer whenever $ n $ has the form $ 2^a 3^b $. It is open for all other values.

See Bar-Natan's page for more.

Bibliography

[BCG] E. R. Berlekamp, J. H. Conway and R. K. Guy, Winning Ways for Your Mathematical Plays, Academic Press, New York 1983.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options