Home » Subject » Graph Theory
Importance: Medium ✭✭
Author(s): Blankenship, Robin
Oporowski, Bogdan
Subject: Graph Theory
Keywords: book embedding
book thickness
Recomm. for undergrads: yes
Posted by: David Wood
on: January 19th, 2009

Let $ G $ be a finite undirected simple graph.

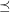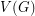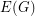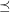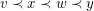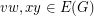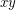A $ k $-page book embedding of $ G $ consists of a linear order $ \preceq $ of $ V(G) $ and a (non-proper) $ k $-colouring of $ E(G) $ such that edges with the same colour do not cross with respect to $ \preceq $. That is, if $ v\prec x\prec w\prec y $ for some edges $ vw,xy\in E(G) $, then $ vw $ and $ xy $ receive distinct colours.

One can think that the vertices are placed along the spine of a book, and the edges are drawn without crossings on the pages of the book.

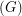The book thickness of $ G $, denoted by bt$ (G) $ is the minimum integer $ k $ for which there is a $ k $-page book embedding of $ G $.

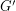Let $ G' $ be the graph obtained by subdividing each edge of $ G $ exactly once.

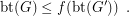
Conjecture   There is a function $ f $ such that for every graph $ G $, $$ \text{bt}(G) \leq f( \text{bt}(G') )\enspace. $$

The conjecture is due to [B099]. The conjecture is true for complete graphs [BO99,EM99,E02]. The conjecture is discussed in depth in [DW05].

Bibliography

*[BO99] Robin Blankenship and Bogdan Oporowski. Drawing Subdivisions Of Complete And Complete Bipartite Graphs On Books, Technical Report 1999-4, Department of Mathematics, Louisiana State University, 1999.

[DW05] Vida Dujmovic and David Wood. Stacks, queues and tracks: Layouts of graph subdivisions. Discrete Mathematics & Theoretical Computer Science 7:155-202, 2005.

[EM99] Hikoe Enomoto and Miki Shimabara Miyauchi. Embedding graphs into a three page book with 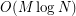$ O(M \log N) $ crossings of edges over the spine. SIAM J. Discrete Math., 12(3):337–341, 1999.

[E02] David Eppstein. Separating thickness from geometric thickness. In Proc. 10th International Symp. on Graph Drawing (GD ’02), pp. 150–161. vol. 2528 of Lecture Notes in Comput. Sci. Springer, 2002.


* indicates original appearance(s) of problem.
1 comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options