 login/create account
login/create account
Blankenship, Robin
Book Thickness of Subdivisions ★★
Author(s): Blankenship; Oporowski
Let  be a finite undirected simple graph.
be a finite undirected simple graph.
A  -page book embedding of
-page book embedding of  consists of a linear order
consists of a linear order 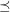 of
of 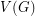 and a (non-proper)
and a (non-proper)  -colouring of
-colouring of 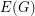 such that edges with the same colour do not cross with respect to
such that edges with the same colour do not cross with respect to 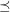 . That is, if
. That is, if 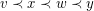 for some edges
for some edges 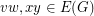 , then
, then  and
and 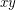 receive distinct colours.
receive distinct colours.
One can think that the vertices are placed along the spine of a book, and the edges are drawn without crossings on the pages of the book.
The book thickness of  , denoted by bt
, denoted by bt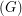 is the minimum integer
is the minimum integer  for which there is a
for which there is a  -page book embedding of
-page book embedding of  .
.
Let 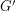 be the graph obtained by subdividing each edge of
be the graph obtained by subdividing each edge of  exactly once.
exactly once.
Conjecture There is a function  such that for every graph
such that for every graph  ,
, 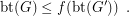
 such that for every graph
such that for every graph  ,
, 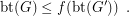
Keywords: book embedding; book thickness

 Drupal
Drupal CSI of Charles University
CSI of Charles University