 login/create account
login/create account
The fatness of a 4-polytope  is defined to be
is defined to be 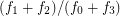 where
where 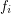 is the number of faces of
is the number of faces of  of dimension
of dimension 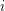 .
.
 so that every convex 4-polytope has fatness at most
so that every convex 4-polytope has fatness at most  ?
? The  -vector of a
-vector of a  -dimensional polytope
-dimensional polytope  is the vector
is the vector  where
where 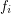 is the number of faces of dimension
is the number of faces of dimension 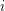 . Let us denote by
. Let us denote by 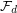 the collection of all
the collection of all  -vectors of convex
-vectors of convex  -dimensional polytopes. Steinitz proved that the set
-dimensional polytopes. Steinitz proved that the set 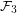 is completely characterized by the following three conditions:
is completely characterized by the following three conditions:
- \item
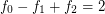 , \item
, \item 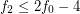 , \item
, \item 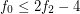 .
. The first of these conditions is Euler's formula. The second and third are easy inequalities which are tight for simplicial (all faces triangles) and simple (all vertices of degree 3) polytopes, respectively.
In sharp contrast to this, the situation for 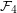 seems to be quite complicated. For instance, it has been shown that
seems to be quite complicated. For instance, it has been shown that 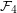 does not contain all elements of
does not contain all elements of 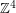 which lie in the convex hull of
which lie in the convex hull of 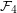 ; i.e.,
; i.e., 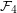 has "holes" in it. For the extreme examples of simple and simplicial polytopes, the
has "holes" in it. For the extreme examples of simple and simplicial polytopes, the  -theorem of Billera-Lee and Stanley gives a complete description of all possible
-theorem of Billera-Lee and Stanley gives a complete description of all possible  -vectors, but in general very little is known.
-vectors, but in general very little is known.

 Drupal
Drupal CSI of Charles University
CSI of Charles University