Home » Subject » Geometry
Importance: High ✭✭✭
Author(s):
Subject: Geometry
Keywords: cube
decomposition
simplex
Recomm. for undergrads: yes
Posted by: mdevos
on: August 6th, 2008
Question   What is the minimum cardinality of a decomposition of the $ n $-cube into $ n $-simplices?

A decomposition of a polytope $ P $ into $ n $-simplices is a set of $ n $-simplices which have pairwise disjoint interiors and have union equal to $ P $. This is also known as a (generalized) triangulation.

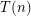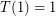Let $ T(n) $ be the minimum cardinality of a decomposition of the $ n $-cube into $ n $-simplices (the answer to our question). It is trivial that $ T(1) = 1 $ and easy to see that 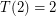$ T(2) = 2 $. A 3-dimensional cube may be decomposed into five simplices by cutting off every other corner as shown in the figure (from [JW]). This division is optimal, so $ T(3) = 5 $.

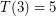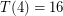Chopping off every other corner of a 4-cube leaves a 16-cell (the 4-dimensional cross-polytope) which can then be decomposed into eight simplices (fix a vertex $ x $ and then take each of the eight 4-simplices formed as the convex hull of $ x $ and a facet which is not incident with $ x $). This is also optimal, so $ T(4) = 16 $. Computer assisted searches have yielded other good decompositions in low dimensions (see [S]).

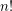The decompositions of the 3 and 4-dimensional cubes described here do not generalize to higher dimensions. However, there is a naive decomposition of an $ n $-cube into $ n! $ simplices. Take the cube to be $ [0,1]^n $ and let $ S $ be the set of all points 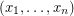$ (x_1,\ldots,x_n) $ for which 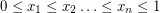$ 0 \le x_1 \le x_2 \ldots \le x_n \le 1 $. 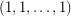Then $ S $ is a simplex contained in our cube which contains the main diagonal from the origin to $ (1,1,\ldots,1) $. Further, by permuting the terms 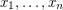$ x_1,\ldots,x_n $ in the chain of inequlities, we get a total of 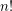$ n! $ simplices which form a decomposition of the cube.

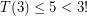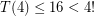This naive decomposition is not optimal in dimensions 3 and 4 since our constructions show $ T(3) \le 5 < 3! $ and $ T(4) \le 16 < 4! $. Haiman [H] found a clever way to lift efficient lower dimensional decompositions to high dimensions thus achieving a significant improvement on our 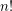$ n! $ upper bound. To state his result precisely, we require another parameter. Let 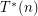$ T^*(n) $ be the minimum cardinality of a decomposition of an $ n $-cube into $ n $-simplices with the following additional constraints:

    \item Every vertex of a simplex is a vertex of the cube. \item The intersection of any two simplices is a face of both of them.

It is immediate that 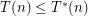$ T(n) \le T^*(n) $, but to the best of our knowledge these parameters may always be identical. Indeed, this is a separate interesting question. Anyway, back to Haiman's bound. He proved that 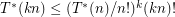$ T^*(kn) \le (T^*(n)/n!)^k (kn)! $. Using this inequality with either the 3 or 4-dimensional example from above would give an improvement on the 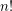$ n! $ upper bound. 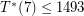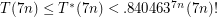However, best known is to plug in $ T^*(7) \le 1493 $, which gives a general upper bound of $ T(7n) \le T^*(7n) < .840463^{7n}(7n)! $.

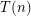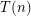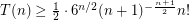A natural lower bound on $ T(n) $ can be obtained by a volume argument. Clearly, $ T(n) $ must be at least the volume of an $ n $-dimensional cube divided by the volume of the largest simplex it contains. Smith [S] improved upon this by moving the argument to hyperbolic space (where the volume of a cube is comparatively much larger than that of a simplex). His volume estimate here yields $ T(n) \ge \frac{1}{2} \cdot 6^{n/2}(n+1)^{- \frac{n+1}{2} } n! $.

Bibliography

[H] M. Haiman, A simple and relatively efficient triangulation of the n-cube, Discr. Comp. Geom. 6, 4 (1991) 287-289.

[JW] Jackson, Frank and Weisstein, Eric W. "Tetrahedron." From MathWorld--A Wolfram Web Resource.

[S] W. Smith, A lower bound for the simplexity of the n-cube via hyperbolic volume.


* indicates original appearance(s) of problem.
add new comment | 1 attachment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options