Home » Subject » Combinatorics
Importance: Medium ✭✭
Author(s): Landman, Bruce M.
Robertson, Aaron
Subject: Combinatorics
Keywords: monochromatic diffsequences
primes
Recomm. for undergrads: no
Posted by: vjungic
on: July 9th, 2008
Question   Is the set of prime numbers 2-accessible?

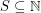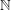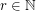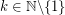A set $ S\subseteq \mathbb{N} $ is $ r $-accessible if for any $ r $-coloring of $ \mathbb{N} $, $ r\in \mathbb{N} $, there exist long monochromatic $ S $-diffsequences, i.e., for any $ k\in \mathbb{N}\backslash \{ 1\} $ there is a monochromatic sequence 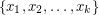$ \{ x_1,x_2,\ldots ,x_k\} $ such that 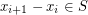$ x_{i+1}-x_i\in S $, for all $ i\in \{ 1,\ldots ,k-1\} $.

The set of primes $ P $ is not 3-accessible. [LR2]

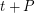Landman and Robertson proved [LR1] that for any odd $ t $, the set $ t+P $ is 2-accessible.

It is known that a 2-coloring of any 33 consecutive positive integers yields a monochromatic 7-term $ P $-diffsequence.

Bibliography

[J] Jungi\'c, Veselin, {\it On a conjecture of Brown concerning accessible sets}, J. Combin. Theory Ser. A 110 (2005), MathSciNet

[KL] Abdollah Khodkar and Bruce M. Landman, {\it Recent progress in Ramsey theory on the integers}, Combinatorial number theory, 305--313, de Gruyter, Berlin, 2007. MathSciNet

[LR1] Bruce M. Landman and Aaron Robertson, {\it Avoiding Monochromatic Sequences With special Gaps}, SIAM J. Discrete Math Vol. 21 (2007), no. 3, 794--801. MathSciNet

*[LR2] Bruce M. Landman and Aaron Robertson, Ramsey Theory on the Integers, Stud. Math. Libr. 24, AMS Providence, RI, 2004.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options